Note
Go to the end to download the full example code.
Integrating constant pressure ignition using SciPy#
Solve a constant pressure ignition problem where the governing equations are implemented in Python.
This demonstrates an approach for solving problems where Cantera’s reactor network model cannot be configured to describe the system in question. Here, Cantera is used for evaluating thermodynamic properties and kinetic rates while an external ODE solver is used to integrate the resulting equations. In this case, the SciPy wrapper for VODE is used, which uses the same variable-order BDF methods as the Sundials CVODES solver used by Cantera.
Requires: cantera >= 2.5.0, scipy >= 0.19, matplotlib >= 2.0
import cantera as ct
import numpy as np
import scipy.integrate
class ReactorOde:
def __init__(self, gas):
# Parameters of the ODE system and auxiliary data are stored in the
# ReactorOde object.
self.gas = gas
self.P = gas.P
def __call__(self, t, y):
"""the ODE function, y' = f(t,y) """
# State vector is [T, Y_1, Y_2, ... Y_K]
self.gas.set_unnormalized_mass_fractions(y[1:])
self.gas.TP = y[0], self.P
rho = self.gas.density
wdot = self.gas.net_production_rates
dTdt = - (np.dot(self.gas.partial_molar_enthalpies, wdot) /
(rho * self.gas.cp))
dYdt = wdot * self.gas.molecular_weights / rho
return np.hstack((dTdt, dYdt))
gas = ct.Solution('h2o2.yaml')
# Initial condition
P = ct.one_atm
gas.TPX = 1001, P, 'H2:2,O2:1,N2:4'
y0 = np.hstack((gas.T, gas.Y))
# Set up objects representing the ODE and the solver
ode = ReactorOde(gas)
solver = scipy.integrate.ode(ode)
solver.set_integrator('vode', method='bdf', with_jacobian=True)
solver.set_initial_value(y0, 0.0)
# Integrate the equations, keeping T(t) and Y(k,t)
t_end = 1e-3
states = ct.SolutionArray(gas, 1, extra={'t': [0.0]})
dt = 1e-5
while solver.successful() and solver.t < t_end:
solver.integrate(solver.t + dt)
gas.TPY = solver.y[0], P, solver.y[1:]
states.append(gas.state, t=solver.t)
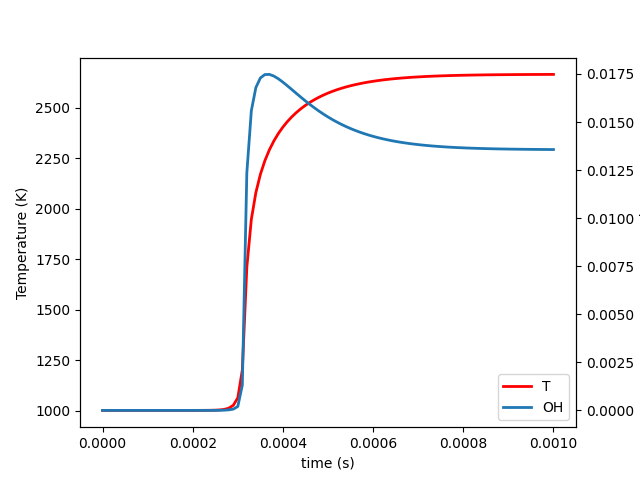
# Plot the results
try:
import matplotlib.pyplot as plt
L1 = plt.plot(states.t, states.T, color='r', label='T', lw=2)
plt.xlabel('time (s)')
plt.ylabel('Temperature (K)')
plt.twinx()
L2 = plt.plot(states.t, states('OH').Y, label='OH', lw=2)
plt.ylabel('Mass Fraction')
plt.legend(L1+L2, [line.get_label() for line in L1+L2], loc='lower right')
plt.show()
except ImportError:
print('Matplotlib not found. Unable to plot results.')
Total running time of the script: (0 minutes 0.175 seconds)

